[백준] 17070 - 파이프 옮기기 1(Java)

문제 파악

https://www.acmicpc.net/problem/17070

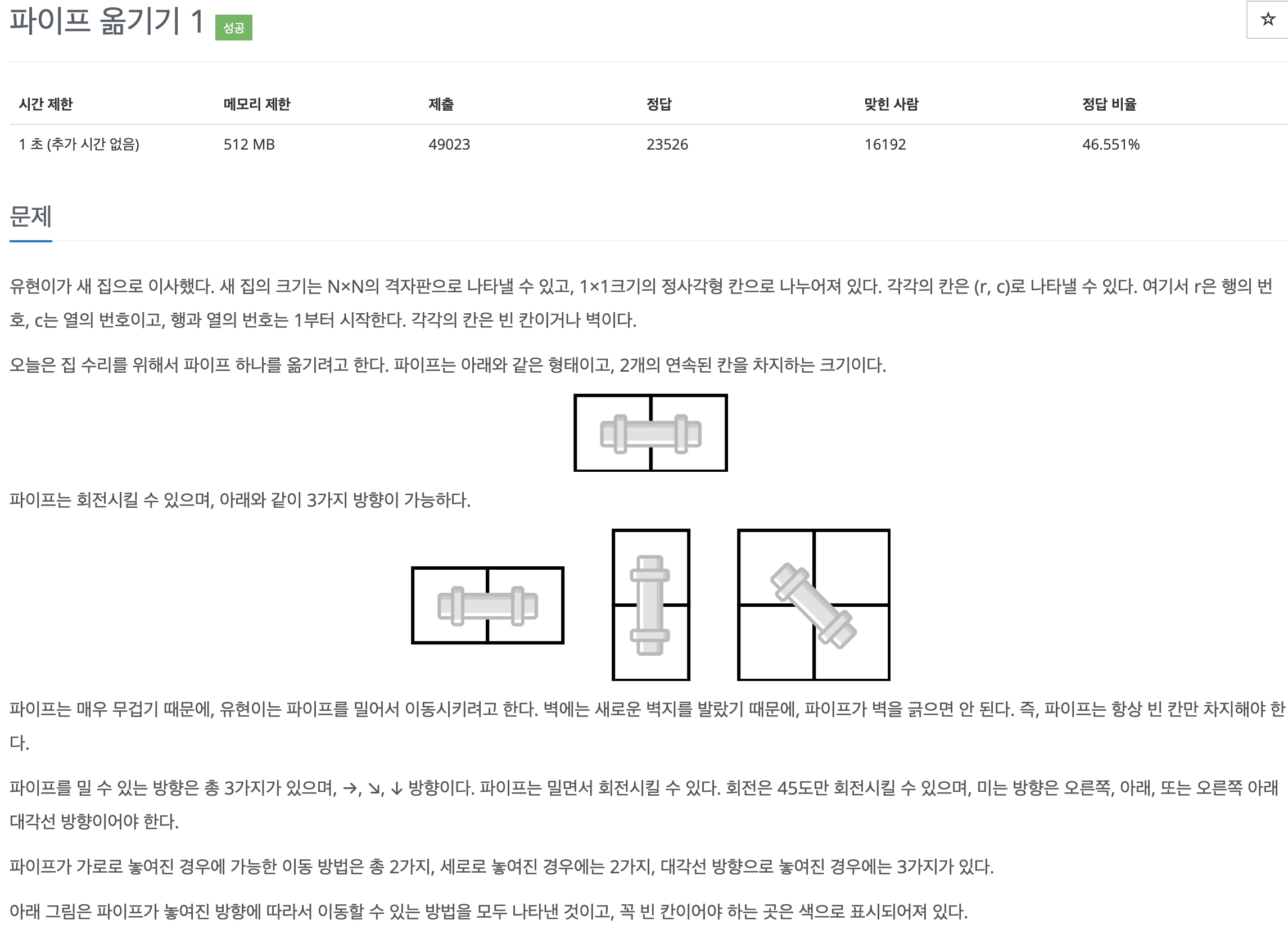
아직 첨부하지 않았지만 파이프를 배치하는 예시도 그림으로 제시해 주는 친절한 문제이다 🥹

풀이

DP로 풀게 되었다.
파이프의 배치를 보면 ↘️ 방향으로 진행되므로, 행과 열이 증가하는 방향으로 조사하며 DP 배열을 업데이트하면 될 것이다.

DP 변수의 선언과 초기화

파이프를 배치하는 경우의 수를 저장하는 3차원 배열을 선언하여 사용해주도록 한다.
이 때 가로 | 세로 | 대각선 파이프가 끝나는 위치를 기준으로 배열을 업데이트해주면 편하다.
따라서 (0,0)에 가로 파이프가 놓여 있는 경우 DP[0][1][가로파이프]에 해당하는 부분이 1이 되겠다.

파이프 배치 방법

앞서 말했듯 파이프의 끝점(↘️ 방향)을 기준으로 한다.

가로 파이프

(R,C) 기준 (R, C-1)에 위치한 가로 파이프, (R,C-1)에 위치한 대각선 파이프의 경우의 수를 더해주자

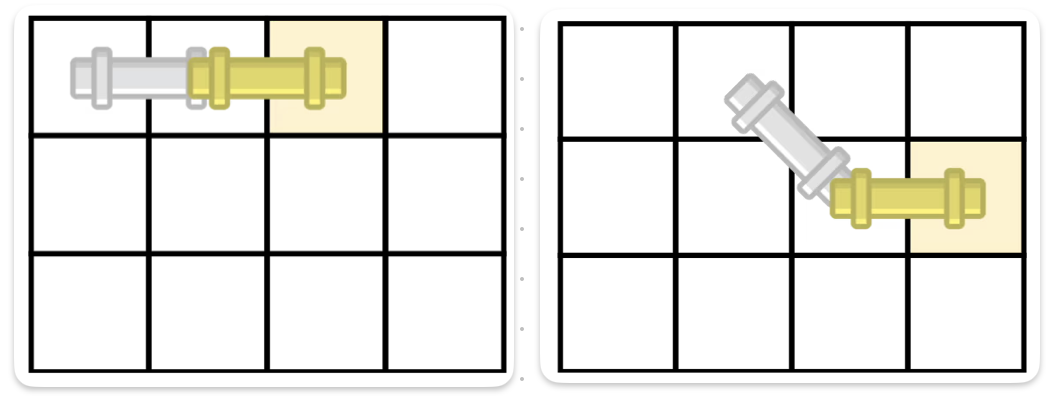
세로 파이프

세로 파이프를 배치하기 위해서는 (R-1, C)에 위치한 세로 파이프, 대각선 파이프의 경우의 수를 더해준다

대각선 파이프

(R-1, C-1)를 출구로 가지는 세로, 가로, 대각선 파이프의 경우의 수를 더해 주자

가로, 세로 파이프와는 달리 파이프를 배치할 때 2X2 에 해당하는 공간에 벽이 있으면 안 된다는 점을 신경쓰며, 벽이 있을 경우 0으로 설정해준다.

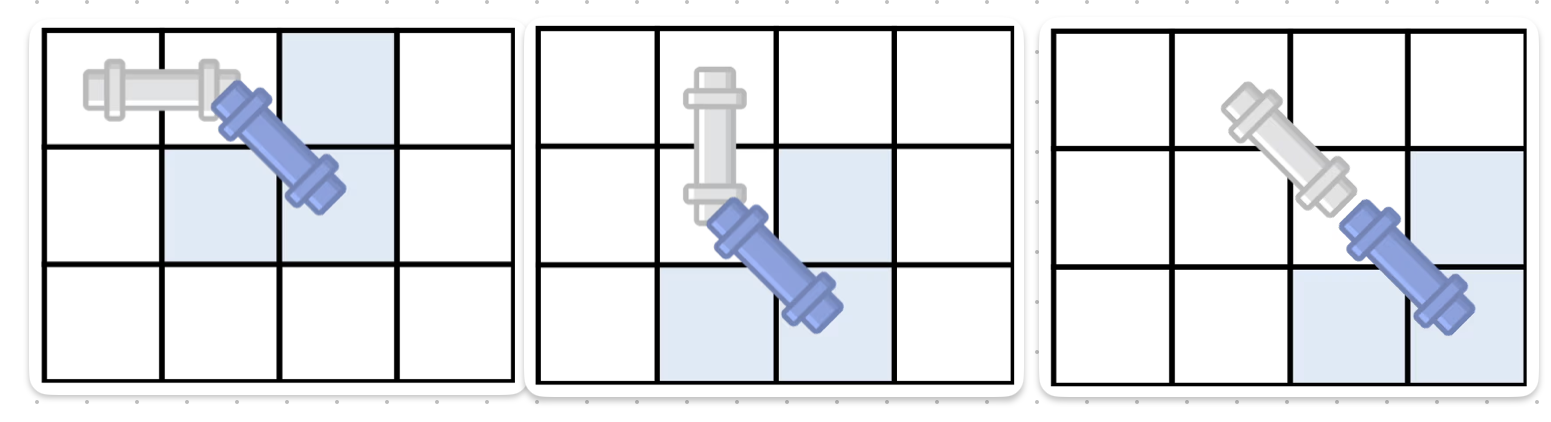
코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());
        boolean[][] canPass = new boolean[N][N]; // N = [3,6]
        int[][][] dp = new int[N][N][3]; // 끝점 기준이며 0 - 가로 파이프, 1 - 세로 파이프, 2 - 대각선 파이프
        for (int r = 0; r < N; r++) {
            StringTokenizer tok = new StringTokenizer(br.readLine(), " ");
            for (int c = 0; c < N; c++) {
                canPass[r][c] = tok.nextToken().equals("0");
            }
        }
        dp[0][1][0] = 1;
        for (int c = 1; c < N; c++) {
            if (!canPass[0][c]) {
                break;
            }
            dp[0][c][0] += dp[0][c - 1][0];
        }
        for (int r = 1; r < N; r++) {
            for (int c = 1; c < N; c++) {
                if (!canPass[r][c]) {
                    continue;
                }
                // 가로
                dp[r][c][0] += dp[r][c - 1][0] + dp[r][c - 1][2];
                // 세로
                dp[r][c][1] += dp[r - 1][c][1] + dp[r - 1][c][2];
                // 대각선
                dp[r][c][2] += (canPass[r - 1][c] && canPass[r][c - 1]) ? dp[r - 1][c - 1][0] + dp[r - 1][c - 1][1] + dp[r - 1][c - 1][2] : 0;
            }
        }
        System.out.println(dp[N - 1][N - 1][0] + dp[N - 1][N - 1][1] + dp[N - 1][N - 1][2]);
    }
}