문제 파악

https://school.programmers.co.kr/learn/courses/30/lessons/258705
어려운 점
보자마자 “DP 문제다” 라고 느껴졌지만, 정확한 규칙을 찾는 데 시간이 꽤 걸렸다.
특히 상태를 어떻게 정의할지 고민하는 과정에서 여러 번 막혔다 ^.ㅠ 🐸
풀이
비트마스크 + DP로 풀어볼까 라고 생각했지만 상태 정의를 비트마스크로 하면 경우의 수가 늘어나 점점 꼬였다 🥲
좀 더 단순한 규칙을 찾아보기로 했다.

먼저 위와 같이 구역을 나눠 규칙을 더 찾아보면 마름모 퍼즐을 아래와 같이 배치하는 경우에만 타 영역을 침범하는 걸 볼 수 있다.
보다시피 이전 영역의 가운데 삼각형 부분에 걸쳐 자리잡고 있다...
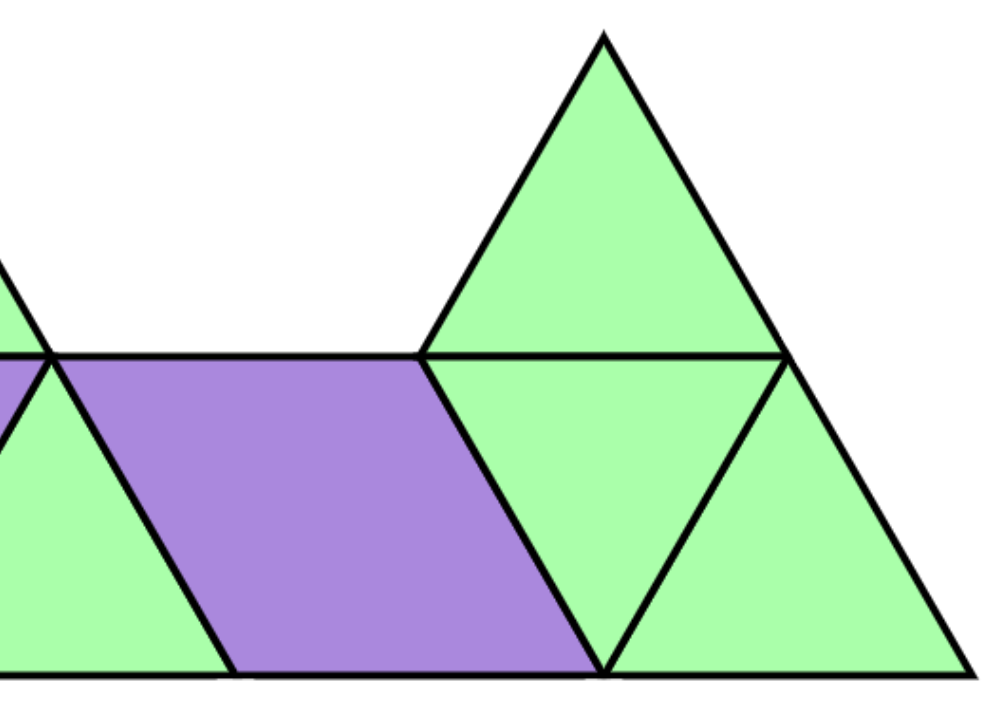
그렇다면 1️⃣중간 지점을 빼고 배치하는 경우의 수와, 2️⃣중간 부분을 채우고 배치하는 경우의 수를 나누자.
다음 구간에서 1️⃣의 경우에는 마름모 퍼즐 ◹◺ 을 선배치한 후 퍼즐을 채워넣고, 2️⃣의 경우에는 일반적으로 퍼즐을 배치하면 되겠다

DP 배열 정의
그럼 해당 아이디어를 바탕으로 2차원 배열 DP[N][2]를 정의해보자.
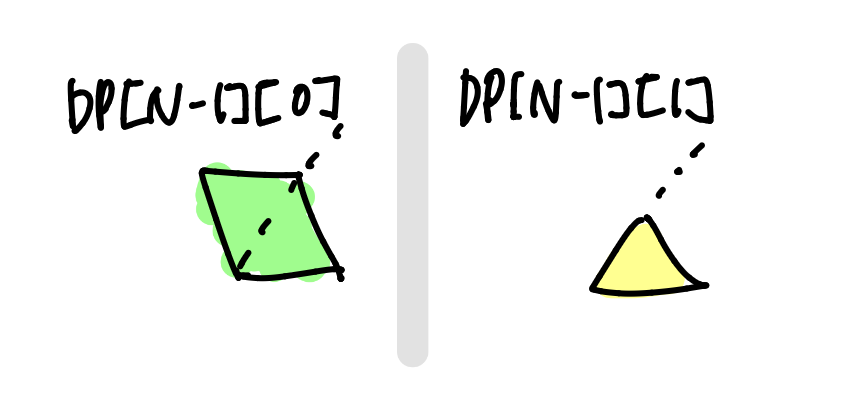
DP[N][0] = 가운데 부분을 채우지 않고 N 구역까지 채우는 경우의 수
DP[N][1] = 가운데 부분을 채우며 N 구역까지 채우는 경우의 수
DP[0] - 초기항
초기 DP[0][0], DP[0][1]은 top[0]에 따라 경우의 수가 달라지므로 나누어 할당해주자
top[0] = 1 의 경우
DP[0][0]은 1가지, DP[0][1]은 3가지 경우의 수를 갖는다
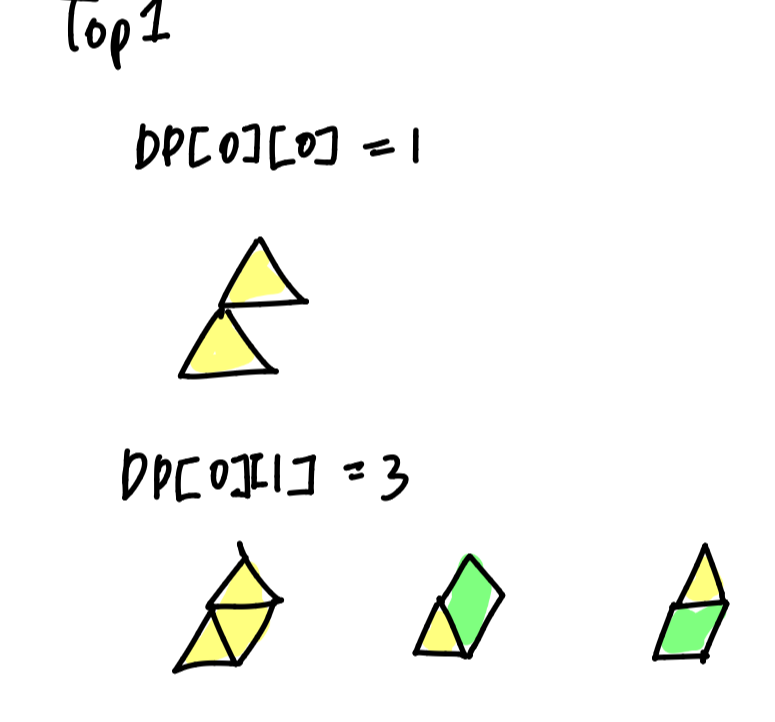
top[0] = 0 의 경우 DP[0]
DP[0][0]은 1가지, DP[0][1]은 2가지 경우의 수를 갖는다
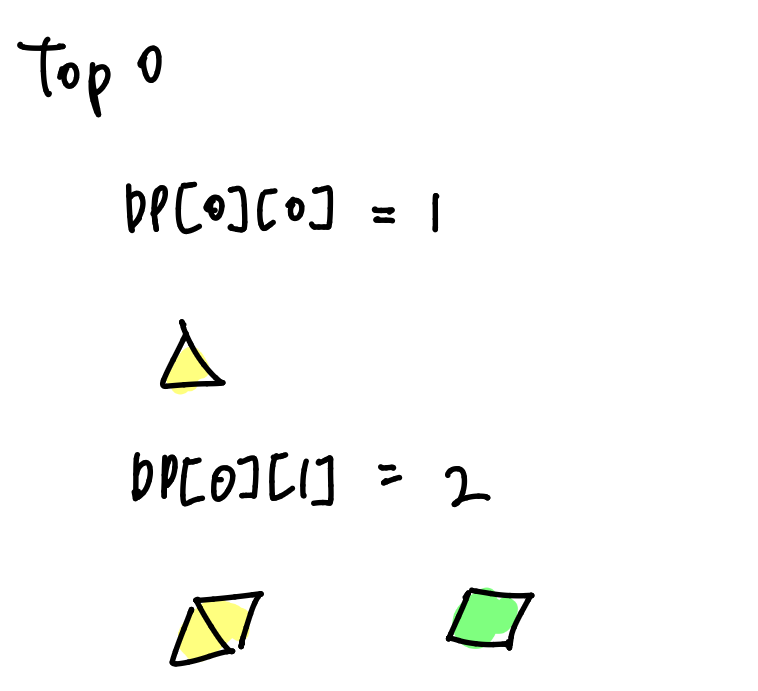
DP[N] - 일반항
다음으로 일반항(DP[N])에서의 점화식을 구하기 위해 경우의 수를 찾아보자
앞과 동일하게 N번째의 가운데를 비우거나 / 비우지 않는 배치를 구상한다
◹◺ 마름모를 아래쪽에 채워넣을 때, 직전 구역에서 가운데가 비어 있는 경우인 DP[N-1][0]을 사용해 준다.
이를 고려하여 경우의 수를 구해 준 다음, 사용한 이전 항(DP[n-1][0] 혹은 DP[n-1][1])을 곱해주면 점화식을 구할 수 있겠다.
추가적으로 현재 top이 0인지, 1인지를 구분하여 배치해주어야 한다.

위의 그림에 퍼즐을 채워넣는다고 생각하고 진행하면 쪼금 편하다
top[N] = 1 일때의 DP[N]
DP[n][0] = DP[n-1][0] + DP[n-1][1]
DP[n][1] = 2 * DP[n-1][0] + 3 * DP[i-1][1]
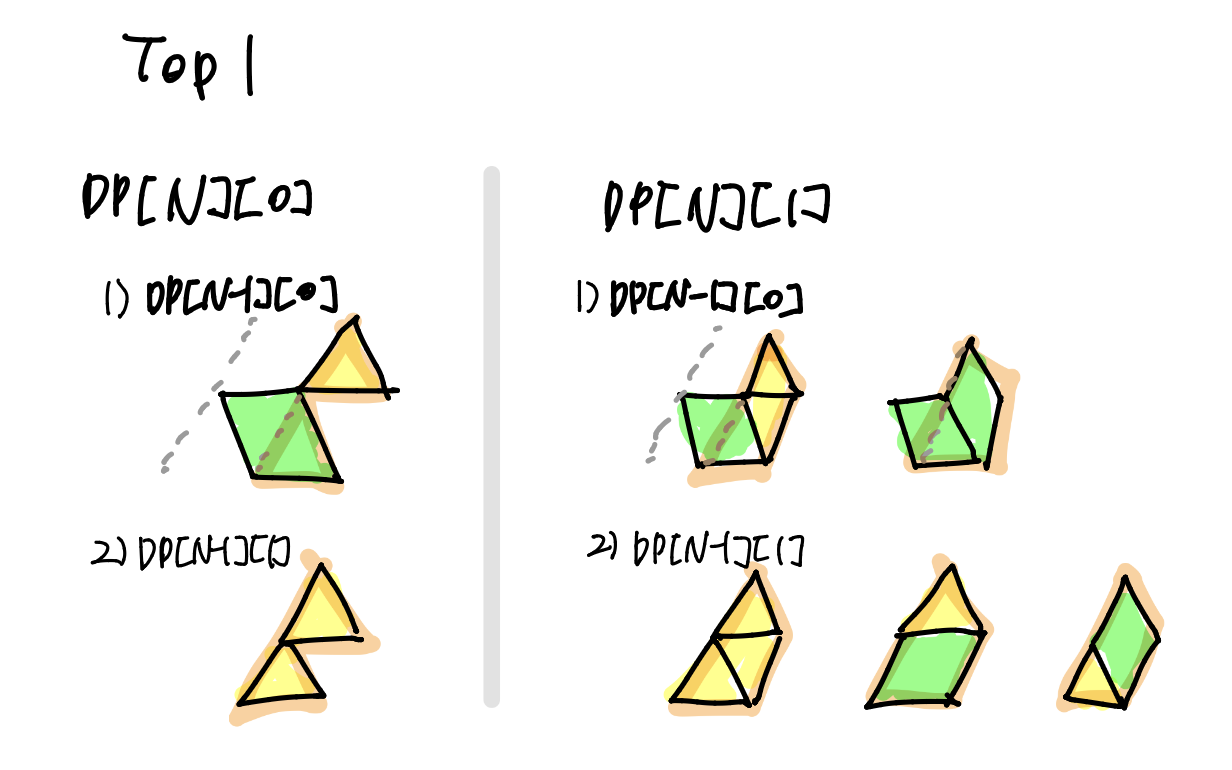
top[N] = 0 일때의 DP[N]
DP[n][0] = DP[n-1][0] + DP[n-1][1]
DP[n][1] = DP[n-1][0] + 2 * DP[N-1][1]
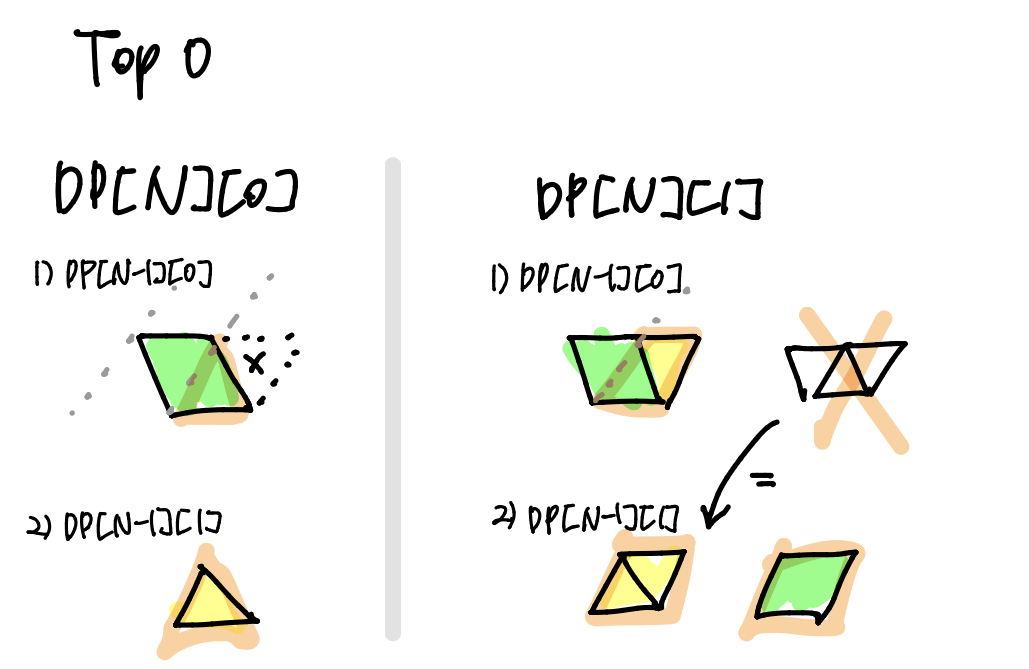
의 점화식을 갖게 된다.
최종 답
가장 오른쪽의 짜투리 세모를 채우기 위해서는
각각 DP[N-1][0]에서 마름모 퍼즐 하나를 채워넣는 경우, DP[N-1][1]에서는 세모 퍼즐을 사용하는 경우 하나씩이므로
DP[N-1][0] + DP[N-1][1] 을 구하면 된다.
점화식만 잘 세우면.. 코드는 매우 간결하다
코드
public class Main {
private static final int DIV = 10007;
public int solution(int n, int[] tops) {
int[][] dp = new int[n][2];
dp[0][0] = 1;
dp[0][1] = tops[0] == 0 ? 2 : 3;
// dp
for (int i = 1; i < n; i++) {
dp[i][0] = (dp[i - 1][0] + dp[i - 1][1]) % DIV;
if (tops[i] == 1) {
dp[i][1] = (2 * dp[i - 1][0] + 3 * dp[i - 1][1]) % DIV;
} else {
dp[i][1] = (dp[i - 1][0] + 2 * dp[i - 1][1]) % DIV;
}
}
return (dp[n - 1][0] + dp[n - 1][1]) % DIV;
}
}
'Algorithm' 카테고리의 다른 글
| [백준] 2169 - 로봇 조종하기(Java) (0) | 2025.12.20 |
|---|---|
| [백준] 3020 - 개똥벌레(Java) (0) | 2025.11.13 |
| [백준] 2493 - 탑(Java) (0) | 2025.11.10 |
| [백준] 1937 - 욕심쟁이 판다 (Java) (4) | 2025.05.15 |
| [백준] 1174 - 줄어드는 수(Java) (1) | 2025.05.08 |